식의 성질을 다루고, 풀기 위해서는 식을 구성하는 수의 성질을 파악해야 한다. 수의 기본 출발점은 \(1\)이다. 인류 문명의 발전과 함께 물건의 개수를 세는 수의 개념이 필요했고, 덧셈은 자연스럽게 확장되었다고 생각할 수 있다. 즉,
\[\eqalign{1&\\2&=1+1\\3&=2+1=1+1+1\\4&=3+1=1+1+1+1\\&\vdots}\]
으로 자연수를 확장할 수 있다.
한편, 반복하는 덧셈은 곱셈으로 바꿔서 계산의 과정을 줄일 수 있고, 표현을 간단하게 할 수도 있다. 즉,
\[\eqalign{4&=2+2=2\times2\\6&=2+2+2=3\times2\\9&=3+3=2\times3\\12&=2+2+2+2+2+2=6\times2\\&\vdots}\]
으로 자연수의 확장을 다시 생각할 수 있다. 그런데, \(1\)이 아닌 수를 이용하여 반복하는 덧셈으로 표현할 수 없는 수들이 존재한다. \(2,\:3,\:5,\:7,\cdots\)과 같은 수들은 곱셈을 이용하여 다른 수를 만드는 데 사용할 수는 있으나 이 수들을 곱셈을 이용하여 표현할 수는 없다. 이러한 수를 소수(素數, prime number)라고 한다. 한자를 풀어보면 바탕이 되는 수라고 할 수 있고, 영어로는 으뜸이 되는 수라고 해석할 수 있다. 소수의 곱셈을 이용하여 다른 수들을 만들어낸다는 점에서 바탕이 되는 수라고 하는 것이 적절해 보인다.
💬 북한에서는 씨수라고 한다.
https://nkinfo.unikorea.go.kr/nkp/term/skNkLangCompare.do?pageIndex=26
소수의 곱셈을 이용해서 만들어내는 수를 합성수(合成數, composite number)라고 한다. 합성을 국어사전에서는 '둘 이상의 것이 합쳐져 하나를 이룸'이라고 정의하고 있다. 소수를 곱해서 만든 수를 합성수라고 부르는 이유라고 하겠다.
\(1\)은 몇 번을 곱해도 \(1\)이므로 바탕이 되는 소수도 아니고, 다른 소수의 곱으로 나타낼 수도 없으므로 합성수도 아니다. 따라서 자연수는 \(1\), 소수, 합성수로 이루어져 있다고 할 수 있다.
- \(1\)은 소수도 합성수도 아니다.
- 소수는 약수가 \(1\)과 자기 자신 뿐이므로 약수의 개수는 \(2\)이다.
- 합성수는 약수가 \(3\)개 이상인 수이다.
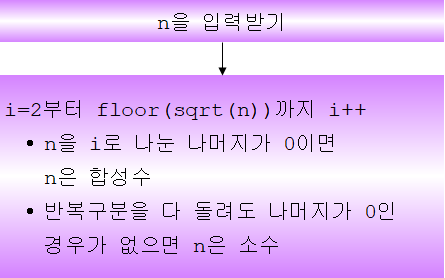
합성수를 만드는 재료가 되는 소수를 찾는 일반적인 방법은 아직까지 발견되지 않았다. 가장 기본적이면서 확실한 방법은 각각의 수를 작은 소수로 나눠보면서 나누어 떨어지는지를 확인하는 것인데 이것을 표로 정리해서 반복 실행하는 방법을 에라토스테네스의 체(Sieve of Eratosthenes)라고 한다. 소수를 찾는 과정이 마치 체를 이용하여 굵은 돌을 걸러내는 것과 같다고 하여 붙여진 이름이다. 순서는 다음과 같다.
찾으려는 범위의 수를 먼저 적는다. 예를 들어 \(1\)부터 \(100\)까지의 소수를 찾으려고 한다면 \(1\)부터 \(100\)까지 일목요연하게 적는다.
- \(1\)은 소수도 합성수도 아니므로 지운다.
- \(2\)에 표시하고 나머지 \(2\)의 배수는 모두 지운다.
- \(3\)에 표시하고 나머지 \(3\)의 배수는 모두 지운다.
- \(4\)는 \(2\)의 배수로 지워졌으니 건너뛴다.
- \(5\)에 표시하고 나머지 \(5\)의 배수는 모두 지운다.
- 이 과정을 반복한다.
- 소수의 제곱수가 찾으려는 범위를 넘으면 지우는 과정을 중단해도 된다. 예를 들어 \(100\)까지 소수를 찾는다면 \(11^2=121\)로 \(100\)을 초과하므로 더 이상 지울 숫자를 찾을 필요 없다.


반복하는 수의 덧셈을 곱셈으로 표현한 것처럼 반복하는 수의 곱셈을 간단하게 표현하는 방법이 있는데 이것을 거듭제곱(exponentiation)이라고 한다. 데카르트(René Descartes)에 의하여 표기법이 완성된 것으로 보고 있는데 다음과 같다.
\[\eqalign {&2\text{의 제곱}\qquad&2^2&=2\times2\\&2\text{의 세제곱}&2^3&=2\times2\times2\\&2\text{의 네제곱}&2^4&=2\times2\times2\times2\\&&&\vdots\\&a\text{의 }n\text{제곱}&a^n&=\underbrace {a\times a \times a \times \cdots \times a}_{n\text{개}} }\]
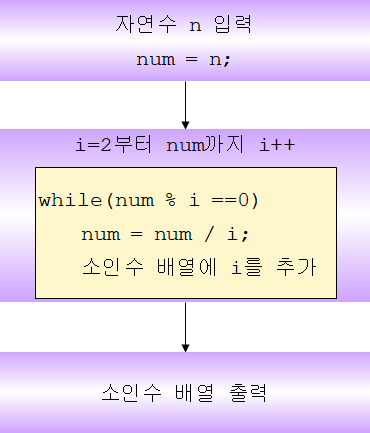
합성수를 소수의 곱으로 표현하는 것을 소인수분해(prime factorization, prime decomposition)라고 하는데 같은 수를 반복해서 곱해야 하므로 거듭제곱을 이용하여 나타낸다. 예를 들어
\[36=4\times9=2\times2\times3 \times3=2^2\times3^2\]
과 같다. 여기에서 \(2\)와 \(3\)을 소인수(prime factor)라고 한다. 즉, 소수를 곱해서 만든 수가 합성수이므로 합성수는 소인수들의 거듭제곱으로 표현할 수 있다. 다시 말해 소인수분해를 하면 약수와 배수를 판단하기 용이해진다. 합성수를 소인수분해할 때는 약수를 이용하지만 순서를 고려하지 않으면 소인수분해는 항상 한 가지로만 표현할 수 있다.
\[\left.\eqalign {60&=2\times30\\&=2\times2\times15\\&=2\times2\times3\times5\\&=2^2\times3\times5 }\quad\right|\quad\left.\eqalign {60&=3\times20\\&=3\times4\times5\\&=3\times2\times2\times5 \\&=2^2\times3\times5}\quad\right|\quad\eqalign {60&=4\times15\\&=2\times2\times3\times5\\&=2^2\times3 \times5\\ &\,}\]
다음은 \(1\)부터 \(300\)까지의 자연수에서 소수를 찾고, 합성수는 소인수분해한 것이다.
\[\left.\eqalign {1&\\
p_1\quad\color{red}{2}&\\
p_2\quad\color{red}{3}&\\
4&=2^2\\
p_3\quad\color{red}{5}&\\
6&=2\times3\qquad\quad\\
p_4\quad\color{red}{7}&\\
8&=2^3\\
9&=3^2\\
10&=2\times5\\
p_5\quad\color{red}{11}&\\
12&=2^2\times3\\
p_6\quad\color{red}{13}&\\
14&=2\times7\\
15&=3\times5\\
16&=2^4\\
p_7\quad\color{red}{17}&\\
18&=2\times3^2\\
p_8\quad\color{red}{19}&\\
20&=2^2\times5\\
21&=3\times7\\
22&=2\times11\\
p_9\quad\color{red}{23}&\\
24&=2^3\times3\\
25&=5^2\\
26&=2\times13\\
27&=3^3\\
28&=2^2\times7\qquad\quad\\
p_{10}\quad\color{red}{29}&\\
30&=2\times3\times5\\
p_{11}\quad\color{red}{31}&\\
32&=2^5\\
33&=3\times11\\
34&=2\times17\\
35&=5\times7\\
36&=2^2\times3^2\\
p_{12}\quad\color{red}{37}&\\
38&=2\times19\\
39&=3\times13\\
40&=2^3\times5\\
p_{13}\quad\color{red}{41}&\\
42&=2\times3\times7\\
p_{14}\quad\color{red}{43}&\\
44&=2^2\times11\\
45&=3^2\times5\\
46&=2\times23\\
p_{15}\quad\color{red}{47}&\\
48&=2^4\times3\\
49&=7^2\\
50&=2\times5^2\\
51&=3\times17\\
52&=2^2\times13\\
p_{16}\quad\color{red}{53}&\\
54&=2\times3^3\\
55&=5\times11\\
56&=2^3\times7\\
57&=3\times19\\
58&=2\times29\\
p_{17}\quad\color{red}{59}&\\
60&=2^2\times3\times5\\
p_{18}\quad\color{red}{61}&\\
62&=2\times31\\
63&=3^2\times7\\
64&=2^6\\
65&=5\times13\\
66&=2\times3\times11\\
p_{19}\quad\color{red}{67}&\\
68&=2^2\times17\\
69&=3\times23\\
70&=2\times5\times7\\
p_{20}\quad\color{red}{71}&\\
72&=2^3\times3^2\\
p_{21}\quad\color{red}{73}&\\
74&=2\times37\\
75&=3\times5^2\\
76&=2^2\times19\\
77&=7\times11\\
78&=2\times3\times13\\
p_{22}\quad\color{red}{79}&\\
80&=2^4\times5\\
81&=3^4\\
82&=2\times41\\
p_{23}\quad\color{red}{83}&\\
84&=2^2\times3\times7\\
85&=5\times17\\
86&=2\times43\\
87&=3\times29\\
88&=2^3\times11\\
p_{24}\quad\color{red}{89}&\\
90&=2\times3^2\times5\\
91&=7\times13\\
92&=2^2\times23\\
93&=3\times31\\
94&=2\times47\\
95&=5\times19\\
96&=2^5\times3\\
p_{25}\quad\color{red}{97}&\\
98&=2\times7^2\\
99&=3^2\times11\\
100&=2^2\times5^2&}\right|
\left.\eqalign {
p_{26}\quad\color{red}{101}&\\
102&=2\times3\times17\\
p_{27}\quad\color{red}{103}&\\
104&=2^3\times13\\
105&=3\times5\times7\\
106&=2\times53\\
p_{28}\quad\color{red}{107}&\\
108&=2^2\times3^3\\
p_{29}\quad\color{red}{109}&\\
110&=2\times5\times11\\
111&=3\times37\\
112&=2^4\times7\\
p_{30}\quad\color{red}{113}&\\
114&=2\times3\times19\\
115&=5\times23\\
116&=2^2\times29\\
117&=3^2\times13\\
118&=2\times59\\
119&=7\times17\\
120&=2^3\times3\times5\\
121&=11^2\\
122&=2\times61\\
123&=3\times41\\
124&=2^2\times31\\
125&=5^3\\
126&=2\times3^2\times7\\
p_{31}\quad\color{red}{127}&\\
128&=2^7\\
129&=3\times43\\
130&=2\times5\times13\\
p_{32}\quad\color{red}{131}&\\
132&=2^2\times3\times11\\
133&=7\times19\\
134&=2\times67\\
135&=3^3\times5\\
136&=2^3\times17\\
p_{33}\quad\color{red}{137}&\\
138&=2\times3\times23\\
p_{34}\quad\color{red}{139}&\\
140&=2^2\times5\times7\\
141&=3\times47\\
142&=2\times71\\
143&=11\times13\\
144&=2^4\times3^2\\
145&=5\times29\\
146&=2\times73\\
147&=3\times7^2\\
148&=2^2\times37\\
p_{35}\quad\color{red}{149}&\\
150&=2\times3\times5^2\\
p_{36}\quad\color{red}{151}&\\
152&=2^3\times19\\
153&=3^2\times17\\
154&=2\times7\times11\\
155&=5\times31\\
156&=2^2\times3\times13\\
p_{37}\quad\color{red}{157}&\\
158&=2\times79\\
159&=3\times53\\
160&=2^5\times5\\
161&=7\times23\\
162&=2\times3^4\\
p_{38}\quad\color{red}{163}&\\
164&=2^2\times41\\
165&=3\times5\times11\\
166&=2\times83\\
p_{39}\quad\color{red}{167}&\\
168&=2^3\times3\times7\\
169&=13^2\\
170&=2\times5\times17\\
171&=3^2\times19\\
172&=2^2\times43\\
p_{40}\quad\color{red}{173}&\\
174&=2\times3\times29\\
175&=5^2\times7\\
176&=2^4\times11\\
177&=3\times59\\
178&=2\times89\\
p_{41}\quad\color{red}{179}&\\
180&=2^2\times3^2\times5\\
p_{42}\quad\color{red}{181}&\\
182&=2\times7\times13\\
183&=3\times61\\
184&=2^3\times23\\
185&=5\times37\\
186&=2\times3\times31\\
187&=11\times17\\
188&=2^2\times47\\
189&=3^3\times7\\
190&=2\times5\times19\\
p_{43}\quad\color{red}{191}&\\
192&=2^6\times3\\
p_{44}\quad\color{red}{193}&\\
194&=2\times97\\
195&=3\times5\times13\\
196&=2^2\times7^2\\
p_{45}\quad\color{red}{197}&\\
198&=2\times3^2\times11\\
p_{46}\quad\color{red}{199}&\\
200&=2^3\times5^2\\}\right|
\eqalign {
201&=3\times67\\
202&=2\times101\\
203&=7\times29\\
204&=2^2\times3\times17\\
205&=5\times41\\
206&=2\times103\\
207&=3^2\times23\\
208&=2^4\times13\\
209&=11\times19\\
210&=2\times3\times5\times7\\
p_{47}\quad\color{red}{211}&\\
212&=2^2\times53\\
213&=3\times71\\
214&=2\times107\\
215&=5\times43\\
216&=2^3\times3^3\\
217&=7\times31\\
218&=2\times109\\
219&=3\times73\\
220&=2^2\times5\times11\\
221&=13\times17\\
222&=2\times3\times37\\
p_{48}\quad\color{red}{223}&\\
224&=2^5\times7\\
225&=3^2\times5^2\\
226&=2\times113\\
p_{49}\quad\color{red}{227}&\\
228&=2^2\times3\times19\\
p_{50}\quad\color{red}{229}&\\
230&=2\times5\times23\\
231&=3\times7\times11\\
232&=2^3\times29\\
p_{51}\quad\color{red}{233}&\\
234&=2\times3^2\times13\\
235&=5\times47\\
236&=2^2\times59\\
237&=3\times79\\
238&=2\times7\times17\\
p_{52}\quad\color{red}{239}&\\
240&=2^4\times3\times5\\
p_{53}\quad\color{red}{241}&\\
242&=2\times11^2\\
243&=3^5\\
244&=2^2\times61\\
245&=5\times7^2\\
246&=2\times3\times41\\
247&=13\times19\\
248&=2^3\times31\\
249&=3\times83\\
250&=2\times5^3\\
p_{54}\quad\color{red}{251}&\\
252&=2^2\times3^2\times7\\
253&=11\times23\\
254&=2\times127\\
255&=3\times5\times17\\
256&=2^8\\
p_{55}\quad\color{red}{257}&\\
258&=2\times3\times43\\
259&=7\times37\\
260&=2^2\times5\times13\\
261&=3^2\times29\\
262&=2\times131\\
p_{56}\quad\color{red}{263}&\\
264&=2^3\times3\times11\\
265&=5\times53\\
266&=2\times7\times19\\
267&=3\times89\\
268&=2^2\times67\\
p_{57}\quad\color{red}{269}&\\
270&=2\times3^3\times5\\
p_{58}\quad\color{red}{271}&\\
272&=2^4\times17\\
273&=3\times7\times13\\
274&=2\times137\\
275&=5^2\times11\\
276&=2^2\times3\times23\\
p_{59}\quad\color{red}{277}&\\
278&=2\times139\\
279&=3^2\times31\\
280&=2^3\times5\times7\\
p_{60}\quad\color{red}{281}&\\
282&=2\times3\times47\\
p_{61}\quad\color{red}{283}&\\
284&=2^2\times71\\
285&=3\times5\times19\\
286&=2\times11\times13\\
287&=7\times41\\
288&=2^5\times3^2\\
289&=17^2\\
290&=2\times5\times29\\
291&=3\times97\\
292&=2^2\times73\\
p_{62}\quad\color{red}{293}&\\
294&=2\times3\times7^2\\
295&=5\times59\\
296&=2^3\times37\\
297&=3^3\times11\\
298&=2\times149\\
299&=13\times23\\
300&=2^2\times3\times5^2}\]
소수가 무한하다는 것은 고대 그리스의 수학자 유클리드(Euclid)의 증명이 유명하다. 그의 증명을 간단하게 요약하면 다음과 같다.
어떤 수 \(N\)이 가장 큰 소수라고 하자. 다시 말해 \(N\)보다 큰 수는 모두 합성수이다. 이제 발견한 모든 소수를 곱한 수 \(N^\prime\)을 생각하자.
\[N^\prime=2\times3\times5\times\cdots\times N\]
그런데 \(P=N^\prime+1\)인 합성수 \(P\)는 어떤 소수로 나누어도 항상 나머지가 \(1\)이므로 가정한 소수로는 소인수분해할 수 없다. 이것은 논리적으로 서로 앞뒤가 맞지 않아 모순이다. 따라서 소수는 무한하다.
소수의 무한함과 그 규칙성이 드러나지 않음, 아주 큰 합성수의 소인수분해의 난해함은 디지털화 된 현대 사회에서는 암호 체계를 유지하는 바탕이 되고 있다.
'잡학다式' 카테고리의 다른 글
| 로마 숫자 (0) | 2021.10.19 |
|---|---|
| 최대공약수와 최소공배수 (0) | 2021.10.13 |
| 자연수의 배수(배수 찾기) (0) | 2021.10.08 |
| 복사용지 규격의 원리와 확대 축소 비율의 규칙에 대하여 (0) | 2021.08.28 |
| [원리합계]예금/적금, 단리/복리 (0) | 2021.08.24 |